Hyunjung Im
Frontend Developer
Tree
2022-04-26
Tree , Binary Search Tree
- Tree 란?
- 왜 Tree 데이터 구조인가?
- Tree 데이터 구조의 기본 용어
- 언제 사용하나요?
- 트리 데이터 구조의 타입
- 트리 데이터 구조의 속성
- 트리 데이터 구조의 Applications
- Big O
- Big O - worst case
- 트리 순회 (Tree Traversal)
- (BST) 검색 작업
- (BST) 삽입 작업
- (BST) 삭제 작업
Tree 란?
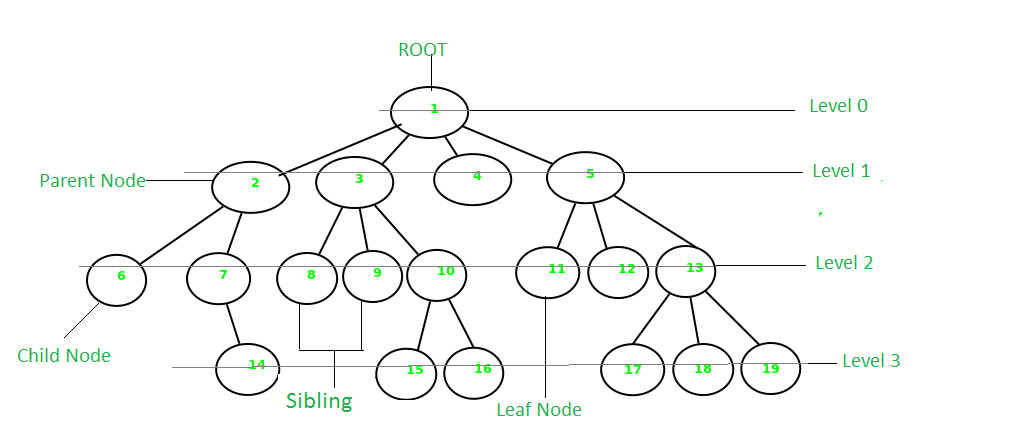트리 구조란 그래프의 일종으로, 여러 노드가 한 노드를 가리킬 수 없는 구조입니다.
엣지로 연결된 노드로 구성되어 있고 서로 다른 두 노드를 잇는 길이 하나뿐인 그래프를 트리라고 부릅니다. 일종의 계층적(Hierarchical) 데이터 구조입니다. 또한 트리 데이터 구조는 서로 연결된 뿌리(roots), 가지(branches), 잎(leaves)을 가지고 있다고 말할 수 있습니다.
트리는 비선형이며 트리의 각 노드가 노드(자식)에 대한 참조 목록인 값을 저장하도록 노드 컬렉션으로 구성된 계층적 비선형 데이터 구조 입니다.
왜 Tree 데이터 구조인가?
배열, linked list, stack, queue 와 같은 다른 데이터 구조는 데이터를 순차적으로 저장하는 선형 데이터 구조입니다. 선형 데이터 구조에서 어떤 연산을 수행하기 위해서는 데이터 크기가 커질수록 시간 복잡도가 증가하게됩니다.
트리 데이터 구조는 비선형 데이터 구조이므로 데이터에 더 빠르고 쉽게 액세스할 수 있습니다.
Tree 데이터 구조의 기본 용어
- Node: 트리에서 데이터를 저장하는 기본 요소
- Edge: 각 Node들이 연결된 선
- Root Node: 트리 맨 위에 있는 노드
- Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node: 어떤 노드의 상위 레벨에 연결된 노드
- Child Node: 어떤 노드의 다음 레벨에 연결된 노드
- Leaf Node: Child Node가 하나도 없는 노드
- Sibling: 동일한 Parent Node를 가진 노드
- Degree of a Node: 해당 노드에 연결된 하위 트리의 총 수를 노드의 차수라고 합니다.
- Depth(or height of a tree): 트리에서 Node가 가질 수 있는 최대 Level
- Depth of a node: 루트에서 노드까지의 엣지 수
- Height of a node: 해당 노드에서 리프까지 가장 긴 경로의 엣지 수
- Internal node: 하나 이상의 자식이 있는 노드를 내부 노드라고 합니다.
언제 사용하나요?
- DOM (Document Object Model)
- File system
- Structure of an organization
- 일반적으로 계층 구조의 경우, 트리 자료구조를 사용하여 구현되었을 때가 많습니다.
- 순서가 있는 데이터(정렬이 되어있는 데이터)를 탐색할 때
- AVL Tree, Red Black Tree are more useful in real scenarios because they are self-balancing.
트리 데이터 구조의 타입
- General tree
- 일반적인 트리 데이터 구조는 노드 수에 제한이 없습니다. 이는 상위 노드가 임의의 수의 하위 노드를 가질 수 있음을 의미합니다.
- Binary tree(이진 트리)
- 이진트리의 노드는 최대 2개의 자식 노드를 가질 수 있습니다.
- Balanced tree
- 왼쪽 서브트리와 오른쪽 서브트리의 높이가 같거나 최대 1 차이가 나는 경우의 트리를 균형 트리 데이터 구조라고 합니다.
- Binary search tree
- 이진 검색 트리는 이름에서 알 수 있듯이 다양한 검색 및 정렬 알고리즘에 사용됩니다. 예로는 AVL 트리와 Red-Black 트리가 있습니다.
- 왼쪽 노드의 값은 부모보다 작고 오른쪽 노드의 값은 부모보다 큽니다.
트리 데이터 구조의 속성
- n개의 노드에 대해 트리의 엣지는 (n-1)과 같습니다.
- The arrow in the structure represents the path. 모든 엣지는 두 개의 노드를 연결합니다.
- 트리 그래프의 두 노드 또는 정점(vertices)은 정확히 하나의 엣지로 연결됩니다.
- 노드의 깊이는 루트 노드에서 노드까지의 경로 길이로 정의됩니다.
트리 데이터 구조의 Applications
- Spanning trees
- 패킷을 목적지로 보내기 위해 라우터에서 사용되는 최단 경로 트리입니다.
- Binary Search Tree
- 정렬된 데이터 스트림을 유지하는 데 도움이 되는 일종의 트리 데이터 구조입니다.
- Storing hierarchical data
- 트리 데이터 구조는 계층적 데이터를 저장하는 데 사용되며, 이는 데이터를 순서의 형태로 배열하는 것을 의미합니다.
- Syntax tree
- 구문 트리는 컴파일러에서 사용되는 프로그램 소스 코드의 구조를 나타냅니다.
- Trie
- 동적 맞춤법 검사를 위한 빠르고 효율적인 방법입니다. 또한 세트 내에서 특정 키를 찾는 데 사용됩니다.
- Heap
- 배열 형태로 표현할 수 있는 트리 데이터 구조이기도 합니다. 우선 순위 대기열을 구현하는 데 사용됩니다.
Big O
- Insertion: O(log n)
- Deletion: O(log n)
- Search: O(log n)
Big O - worst case
- Insertion: O(n)
- Deletion: O(n)
- Search: O(n)
트리 순회 (Tree Traversal)
트리를 순회한다는 것은 트리의 모든 노드를 방문하는 것을 의미합니다. 예를 들어 트리의 모든 값을 추가하거나 가장 큰 값을 찾을 수 있습니다. 이러한 모든 작업을 수행하려면 트리의 각 노드를 방문해야 합니다.
배열, 스택, 큐 및 연결 리스트와 같은 선형 데이터 구조는 데이터를 읽는 방법이 한 가지뿐입니다. 그러나 트리와 같은 계층적 데이터 구조는 다른 방식으로 탐색할 수 있습니다.
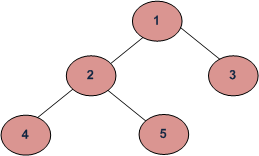
Inorder 중위 순회 (Left, Root, Right)
- 4 2 5 1 3
Preorder 선주문 순회 (Root, Left, Right)
- 1 2 4 5 3
Postorder 후위 순회(Left, Right, Root)
- 4 5 2 3 1
Binary Search Tree
- 정렬된 숫자 목록을 빠르게 유지할 수 있는 데이터 구조입니다. Tree 중에 제일 유명한 구조라고 합니다.
- 각 트리 노드에는 최대 두 개의 자식이 있기 때문에 이진 트리라고 하고 O(log n) 시간 동안 숫자의 존재를 검색하는 데 사용할 수 있기 때문에 검색 트리라고 합니다.
- 노드의 왼쪽 하위 트리에는 노드의 키보다 작은 키를 가진 노드만 포함됩니다.
- 노드의 오른쪽 하위 트리에는 노드 키보다 큰 키가 있는 노드만 포함됩니다.
- 왼쪽 및 오른쪽 하위 트리는 각각 이진 검색 트리여야 하고 중복 노드가 없어야 합니다.
- 각 노드의 두 하위 트리는 모두 BST입니다. 위의 속성을 가집니다.
- 위의 속성은 검색, 최소값, 최대값과 같은 작업을 빠르게 수행할 수 있도록 키 간의 순서를 제공합니다. 순서가 없으면 주어진 키를 검색하기 위해 모든 키를 비교해야 할 수 있습니다.
(BST) 검색 작업
정렬된 배열이 있다면 이진 검색을 수행할 수 있습니다. 배열에서 숫자를 검색하려고 한다고 가정해보겠습니다. 이진 검색에서는 먼저 전체 목록을 검색 공간으로 정의합니다. 이제 검색할 숫자 또는 검색할 요소를 검색 공간의 중간 요소(중앙값)와 비교하고 검색되는 레코드가 중간 요소보다 작으면 왼쪽 절반으로 검색하고 그렇지 않으면 오른쪽 절반에서 검색합니다. 이진 검색에서 ‘n’으로 시작하고 중간요소가 우리가 찾고 있는 요소가 아닐 경우 검색 공간을 n/2 로 줄입니다. 검색을 완료할 때 까지 검색 공간을 계속 줄여나갑니다.
트리가 균형을 이루고 있으면(균형 노드) 검색 공간 ‘n’으로 시작합니다. 노드를 제거하고 하위 트리 중 하나를 버릴 때 ‘n/2’노드를 버리므로 검색 공간이 ‘n/2’로 줄어듭니다. 다음 단계에서 검색 공간을 ‘n/4’로 줄이고 요소를 찾거나 검색 공간이 하나의 노드로 줄어들 때까지 반복합니다.
<script>
// A utility function to search
// a given key in BST
function search(root, key)
{
// Base Cases: root is null
// or key is present at root
if (root == null ||
root.key == key)
return root;
// Key is greater than root's key
if (root.key < key)
return search(root.right, key);
// Key is smaller than root's key
return search(root.left, key);
}
// This code is contributed by rrrtnx.
</script>(BST) 삽입 작업
올바른 위치에 값을 삽입하는 것은 왼쪽 하위 트리가 루트보다 작고 오른쪽 하위 트리가 루트보다 크다는 규칙을 유지하려고 하기 때문에 검색과 유사합니다.
값에 따라 오른쪽 하위 트리 또는 왼쪽 하위 트리로 계속 이동하고 왼쪽 또는 오른쪽 하위 트리가 null인 지점에 도달하면 거기에 새 노드를 넣습니다.
<script>
// javascript program to demonstrate
// insert operation in binary
// search tree
/*
* Class containing left and right child of current node and key value
*/
class Node {
constructor(item) {
this.key = item;
this.left = this.right = null;
}
}
// Root of BST
var root = null;
// This method mainly calls insertRec()
function insert(key) {
root = insertRec(root, key);
}
/*
* A recursive function to insert a new key in BST
*/
function insertRec(root , key) {
/*
* If the tree is empty, return a new node
*/
if (root == null) {
root = new Node(key);
return root;
}
/* Otherwise, recur down the tree */
if (key < root.key)
root.left = insertRec(root.left, key);
else if (key > root.key)
root.right = insertRec(root.right, key);
/* return the (unchanged) node pointer */
return root;
}
// This method mainly calls InorderRec()
function inorder() {
inorderRec(root);
}
// A utility function to
// do inorder traversal of BST
function inorderRec(root)
{
if (root != null) {
inorderRec(root.left);
document.write(root.key+"<br/>");
inorderRec(root.right);
}
}
// Driver Code
/* Let us create following BST
50
/ 30 70
/ / 20 40 60 80 */
insert(50);
insert(30);
insert(20);
insert(40);
insert(70);
insert(60);
insert(80);
// print inorder traversal of the BST
inorder();
// This code is contributed by Rajput-Ji
</script>(BST) 삭제 작업
이진 검색 트리에서 노드를 삭제하는 세 가지 경우가 있습니다.
- 삭제할 노드가 리프 노드인 경우
- 이 경우 트리에서 노드를 삭제하기만 하면 됩니다.
- 삭제할 노드가 하나의 자식 노드를 가지는 경우
- 해당 노드를 자식 노드로 바꿉니다.(복제합니다)
- 원래 위치에서 자식 노드를 제거합니다.
- 삭제할 노드에 두 개의 자식이 있는 경우
- 해당 노드의 inorder 후임자를 가져옵니다.
- 노드를 inorder 후속 작업으로 교체합니다.
- 원래 위치에서 inorder 후속 작업을 제거합니다.
<script>
// Javascript program to demonstrate
// delete operation in binary
// search tree
class Node
{
constructor(item)
{
this.key = item;
this.left = this.right = null;
}
}
// Root of BST
let root=null;
// This method mainly calls deleteRec()
function deleteKey(key)
{
root = deleteRec(root, key);
}
/* A recursive function to
delete an existing key in BST
*/
function deleteRec(root,key)
{
/* Base Case: If the tree is empty */
if (root == null)
return root;
/* Otherwise, recur down the tree */
if (key < root.key)
root.left = deleteRec(root.left, key);
else if (key > root.key)
root.right = deleteRec(root.right, key);
// if key is same as root's
// key, then This is the
// node to be deleted
else {
// node with only one child or no child
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// node with two children: Get the inorder
// successor (smallest in the right subtree)
root.key = minValue(root.right);
// Delete the inorder successor
root.right = deleteRec(root.right, root.key);
}
return root;
}
function minValue(root)
{
let minv = root.key;
while (root.left != null)
{
minv = root.left.key;
root = root.left;
}
return minv;
}
// This method mainly calls insertRec()
function insert(key)
{
root = insertRec(root, key);
}
/* A recursive function to
insert a new key in BST */
function insertRec(root,key)
{
/* If the tree is empty,
return a new node */
if (root == null) {
root = new Node(key);
return root;
}
/* Otherwise, recur down the tree */
if (key < root.key)
root.left = insertRec(root.left, key);
else if (key > root.key)
root.right = insertRec(root.right, key);
/* return the (unchanged) node pointer */
return root;
}
// This method mainly calls InorderRec()
function inorder()
{
inorderRec(root);
}
// A utility function to do inorder traversal of BST
function inorderRec(root)
{
if (root != null) {
inorderRec(root.left);
document.write(root.key + " ");
inorderRec(root.right);
}
}
// Driver Code
/* Let us create following BST
50
/ 30 70
/ / 20 40 60 80 */
insert(50);
insert(30);
insert(20);
insert(40);
insert(70);
insert(60);
insert(80);
document.write(
"Inorder traversal of the given tree<br>");
inorder();
document.write("<br>Delete 20<br>");
deleteKey(20);
document.write(
"Inorder traversal of the modified tree<br>");
inorder();
document.write("<br>Delete 30<br>");
deleteKey(30);
document.write(
"Inorder traversal of the modified tree<br>");
inorder();
document.write("<br>Delete 50<br>");
deleteKey(50);
document.write(
"Inorder traversal of the modified tree<br>");
inorder();
// This code is contributed by avanitrachhadiya2155
</script>참조 및 출처